Exercise 2

Consider the points

\[ A = (\frac{\pi}{2}, -\frac{\pi}{2}, F(\frac{\pi}{2}, -\frac{\pi}{2})) \] \[ B = (-\frac{\pi}{2}, \frac{\pi}{2}, F(-\frac{\pi}{2}, \frac{\pi}{2})) \] \[ C = (-\frac{\pi}{2}, -\frac{\pi}{2}, F(-\frac{\pi}{2}, -\frac{\pi}{2})) \]

---

\[ F(x, y) = \sin x + \sin y \] \[\frac{\partial F}{\partial x} = \cos x\] \[\frac{\partial F}{\partial y} = \cos y\] \[\frac{\partial^2 F}{\partial x^2} = - \sin x \] \[\frac{\partial^2 F}{\partial y^2} = - \sin y \] \[\frac{\partial^2 F}{\partial x \, \partial y} = \frac{\partial^2 F}{\partial y \, \partial x} = 0 \]

Point A:

\[\frac{\partial F}{\partial x} = \cos \left( \frac{\pi}{2} \right) = 0 \] \[\frac{\partial F}{\partial y} = \cos \left( -\frac{\pi}{2} \right) = 0 \]

\[ \det H = (- \sin \left( \frac{\pi}{2} \right) ) \, (- \sin \left( -\frac{\pi}{2} \right) ) - 0 = (-1) \, (+1) = -1 \lt 0 \]

Point A is a saddle point.

Point B: \[ \det H = (- \sin \left( -\frac{\pi}{2} \right) ) \, (- \sin \left( \frac{\pi}{2} \right) ) - 0 = (+1) \, (-1) = -1 \lt 0 \]

Point B is also a saddle point.

Point C: \[ \det H = (- \sin \left( -\frac{\pi}{2} \right) ) \, (- \sin \left( -\frac{\pi}{2} \right) ) - 0 = 1 \gt 0 \]

We calculate the trace of the Hesse matrix to decide, whether wie have a minimum or maximum.
\[ \mathrm{Tr} \, H = (- \sin \left( -\frac{\pi}{2} \right) ) + (- \sin \left( -\frac{\pi}{2} \right) ) = 1 +1 = 2 \gt 0 \] Point C is a local minimum.

The position of the points is shown in the following function plot:

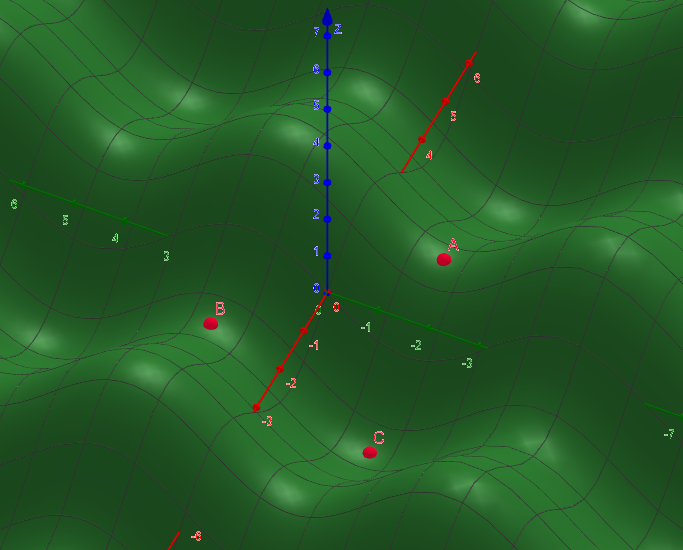
For an interactive 3D graphic, click here. You can also see Point D, which was examined in the textbook (local maximum).

---

We now examine the function \[ F(x, y) = \cos x + \cos y \]

\[\frac{\partial F}{\partial x} = -\sin x\] \[\frac{\partial F}{\partial y} = -\sin y\]

The following applies to point A: \[\frac{\partial F}{\partial x} = -\sin \left( \frac{\pi}{2} \right) = -1 \] \[\frac{\partial F}{\partial y} = -\sin \left( -\frac{\pi}{2} \right) = 1 \] Hence, the point A is not a stationary point.

The following applies to point B: \[\frac{\partial F}{\partial x} = -\sin \left( -\frac{\pi}{2} \right) = 1 \] \[\frac{\partial F}{\partial y} = -\sin \left( \frac{\pi}{2} \right) = -1 \] Hence, point B is not a stationary point.

The following applies to point C: \[\frac{\partial F}{\partial x} = -\sin \left( -\frac{\pi}{2} \right) = 1 \] \[\frac{\partial F}{\partial y} = -\sin \left( -\frac{\pi}{2} \right) = 1 \] Point C is not a stationary point.